Age of the Earth Series - 2

Lecture 2 - Complex Dating Methods

In this lecture, we'll go through the various more complex methods of radiometric dating - talking first about Argon-Argon Plateaus, second about isochron methods, and lastly about the Uranium-Lead Concordia Discordia method, the most complex of all.

These methods of dating are extremely powerful, and build in clever mechanisms to test or eliminate the so-called "assumptions" that creationists often criticise geochronologists for making. That's why it's very important to understand them, and to read this lecture carefully before we go on to lecture 3 - where we will show creationist arguments against radiometric dating to be false.

The Argon-Argon Plateau

We talked in lecture 1 about the K-Ar method of dating - comparing the Potassium and Argon in a rock to find its age. This method uses exactly the same parent and daughter isotopes as the potassium-argon method. In effect, it is a different way of telling time from the same clock. Instead of simply comparing the total potassium with the non-air argon in the rock, this method has a way of telling exactly what and how much argon is directly related to the potassium in the rock. Even though it has been around for nearly half a century, the argon-argon method is seldom discussed by groups critical of dating methods.

In the argon-argon method the rock is placed near the center of a nuclear reactor for a period of hours. A nuclear reactor emits a very large number of neutrons, which are capable of changing a small amount of the potassium-39 into argon-39. Argon-39 is not found in nature because it has only a 269-year half-life. The rock is then heated in a furnace to release both the argon-40 and the argon-39 (representing the potassium) for analysis. The heating is done at incrementally higher temperatures and at each step the ratio of argon-40 to argon-39 is measured. In other words, the sample is heated in steps, say 10 degrees, and for each step, how much Ar-40 and Ar-39 that is dislodged is measured.

If the argon-40 is from decay of potassium within the rock, it will come out at the same temperatures as the potassium-derived argon-39 and in a constant proportion. On the other hand, if there is some excess argon-40 in the rock it will cause a different ratio of argon-40 to argon-39 for some or many of the heating steps, so the different heating steps will not agree with each other. In other words, Ar-40 / Ar-39 should be constant for each step, unless Ar-40 has either been added or subtracted from the rock during the time it's been existent. From this we form the Argon-Argon Plateau:



In this sample, a real sample by the way, the Ar40/Ar39 ratio is fairly constant over the temperature steps. This means the rock has not been disturbed, and we have taken, in this case, 25 different and independent measurements of age that have all come out the same. This is a very powerful evidence that the rock is as old as the method claims. It also tests the assumption that argon has not been added or taken away from the rock.

It also means that we can use this method on partially metamorphised rocks. If a rock has gone through a period of heating - but only been partially melted, the argon-40 at the lower temperature steps will have leaked away. But the argon-40 that was harder to dislodge, that only came out at the higher temperature steps, will have remained constant. We will then get a partial-plateau - with lower ratios at the lower temperature steps, but then a constant plateau at higher temperature steps. This method therefore gives us a way of measuring age even in rocks that have been partially metamorphised.

It also tells us definitively if a rock has been tampered with. Here is a "bad" Ar-Ar plateau for reference:



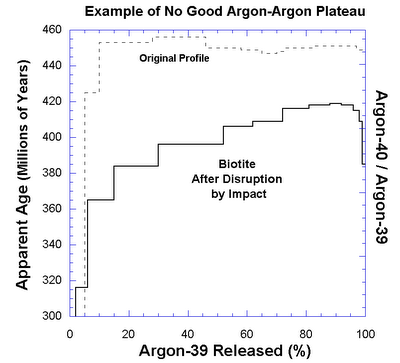
As you can see - the plateau is never constant. Although more of the harder to get out Argon-40 remains at higher temperature, the plateau is never truly flat. This method tells us when a rock is unsuitable for dating then, because argon has been leached. Inspirational stuff. God bless science.

Isochron Methods

In nearly all of the dating methods, except potassium-argon and the associated argon-argon method, there is always some amount of the daughter product already in the rock when it cools. Using these methods is a little like trying to tell time from an hourglass that was turned over before all of the sand had fallen to the bottom.

However one can think of ways to correct for this in an hourglass: One could make a mark on the outside of the glass where the sand level started from and then repeat the interval with a stopwatch in the other hand to calibrate it. Or if one is clever she or he could examine the hourglass' shape and determine what fraction of all the sand was at the top to start with. By knowing how long it takes all of the sand to fall, one could determine how long the time interval was. Similarly, there are good ways to tell quite precisely how much of the daughter product was already in the rock when it cooled and hardened.

In the rubidium-strontium method, rubidium-87 decays with a half-life of 48.8 billion years to strontium-87. Strontium has several other isotopes that are stable and do not decay. When the rock first cools, all parts of the rock have the same strontium-87/strontium-86 ratio because the isotopes were mixed in the magma - and because Sr-87 and Sr-86 are chemically indistinguishable - a mineral cannot distinguish chemically between them. At the same time, some of the minerals in the rock have a higher rubidium/strontium ratio than others. Rubidium has a larger atomic diameter than strontium, so rubidium does not fit into the crystal structure of some minerals as well as others. In other words, Rubidium is chemically distinguishable from Strontium. Therefore the Rb-87/Sr-86 ratio will vary from mineral to mineral. Over time, the Rb-87/Sr-86 ratio decreases as Rb-87 decays to Sr-87. Similarly, the Sr-87/Sr-86 ratio increases over time, as Sr-87 is formed from Rb-87.



The result of this is an isochron, as seen above. This is a plot, for several different minerals, of Sr-87/Sr-86 on the Y-axis and Rb-87/Sr-86 on the X-axis. At the start, you will have a straight flat line, because although there will be different Rb-87/Sr-86 ratios for different minerals, the Sr-87/Sr-86 ratio will be the same, as these are chemically indistinguishable. As time goes on, you will get increasing slopes of line, like this:



The gradient of the line is therefore proportional to the age. Notice also that where the line cuts the Y-axis, we get the exact starting ratios of all the elements, in other words, this method tells us directly what the elemental composition of a rock was to start off with. Enthusiasts can write to me and I'll send them the mathematics behind deriving the age from the gradient.

But the most clever thing about this method is the fact that, if any of our assumptions about the rock are wrong - if the rock has been interfered with - if elements have spread or scattered or left or entered - we won't get a straight line. The very existence of a straight line is proof, in and of itself, that our assumptions were correct.

In a few very rare instances the rubidium-strontium method has given straight lines that give wrong ages. This can happen when the rock being dated was formed from magma that was not well mixed, and which had two distinct batches of rubidium and strontium. One magma batch had rubidium and strontium compositions near the upper end of a line, and one batch had compositions near the lower end of the line.

In this case, the minerals all got a mixture of these two batches, and their resulting composition ended up near a line between the two batches. This is called a two-component mixing line. It is a very rare occurrence in these dating mechanisms, but at least thirty cases have been documented among the tens of thousands of rubidium-strontium dates made.

However, there is a mathematical test (the Reciprocal test) for mixing lines - plus exactly half of all mixing lines are negative - and anyhow, if a two-component mixture is suspected, a second dating method can be used to confirm or disprove the rubidium-strontium date. The agreement of several dating methods is the best fail-safe way of dating rocks - because mixing lines do not agree with other dating methods. So other than mixing, for which we can test and that we know is rare - this is an excellent method of telling the time.

Uranium-Lead Concordia/Discordia

The U-Pb method relies on the decays of U-235 and U-238. These two parent isotopes undergo series decay involving several intermediate radioactive daughter isotopes before the stable daughter product is reached. We have already covered the basic U-Pb method in Lecture 1.

Two simple independent “age” calculations can be made from the two U-Pb decays: U-238 to Pb-206, and U-235 to Pb-207. However, what if lead has leaked out? We found out in lecture 1 that the minerals that Uranium-Lead dating is performed with, like zircons, chemically exclude lead - that also means that during metamorphism and heating lead tends to leak out, giving an artificially young age. How can we get around this problem?

The answer is using a Concordia/Discordia plot. The U-Pb concordia-discordia method circumvents the problem of lead loss in discordant systems and provides an internal check on reliability. This method involves the U-238 and U-235 decays and is used in such minerals as zircon, a common accessory mineral in igneous rocks, that contains uranium but no or negligible initial lead. This latter requirement can be checked, if necessary, by checking for the presence of Pb- 204, which would indicate the presence and amount of initial lead.

In a closed lead-free system, a point representing the 206Pb/238U and 2O7Pb/235U ratios will plot on a curved line known as concordia. The location of the point on concordia depends only on the age of the sample:



In other words, a rock that has not undergone any deformation or metamorphism or leaching will lie on a concordia plot - this means that both U-235 and U-238 methods are in agreement on age, basically. As the rock gets older, it progresses up the concordia plot.

If at some later date (say, 2.5 billion years after formation) the sample loses lead in an episodic event, the point will move off of concordia along a straight line toward the origin (again, the maths of this I'll send to the enthusiast). At any time after the episodic lead loss (say, 1 billion years later), the point Q in the last diagram will lie on a chord to the concordia connecting the original age of the sample and the age of the lead loss episode. As you can see in the diagram, the chord intercepts the concordia at 1 billion years (the time between the last metamorphic event and present day) and 3.5 billion years (the true age of the sample).

This chord is called discordia. If we now consider what would happen to several different samples, say different zircons, from the same rock, each of which lost differing amounts of lead during the episode, we find that at any time after the lead loss, say today, all of the points for these samples will lie on discordia:



As we can see, by drawing the concordia and plotting the discordia from measurements, we can now find the true age of the rock and when the metamorphic event that caused the discordia occured. This is a very powerful method of dating therefore - not only is it self-checking of assumptions - it is actually built specifically to deal with open system behaviour. As we will see in lecture 3 - creationists complain that dating methods have to assume a closed system - that no elements will leak in or out of the sample during the time of its existence. We now know that isochron methods and Ar-Ar methods can handle this - now we've learnt that U-Pb Concordia/Discordia is actually built specifically to deal with this. By the way, the above graph is from a real sample, from the Morton Gneiss, Minn. This rock was also measured at around 3.6 billion years old by several other dating methods.

Dating with multiple methods

As you can see from the results below, amazingly concordant dates are a common feature of radiometric dating using many different methods. These results are from the Amitsoq Gneisses of Western Greenland:



In this case, the gneisses were dated several times using U-Pb, Lead-Lead (another name for Concordia/Discordia methods), Rb-Sr isochron methods, and a couple of lesser used isochron methods, lutetium-hafnium and samarium-neodymium. All the dates agreed to within bounds of error with an age of 3.61 billion years old. The different methods of completely independent, there is no reason that they should agree other than that they represent the real age of the rocks. We will talk about such fallacious creationist claims that these similar results could be caused by a speeding up of radioactive decay rates in lecture 3.

However, that aside, dating with many methods which come up with the same result is a hugely powerful evidence that the earth really is very old. The oldest rocks yet found are about 4.3 billion years old, in Western Australia, making scientists conclude that the earth itself is about 4.5 - 4.6 billion years old in total, giving time for some cooling and rock formation. This age could move back as older rocks are found.

I hope this gives you a good insight into the complex methods of radiometric dating, and that it was not too complex to follow.